HISTORIA DE TEORÍA DE JUEGOS

La teoría de juegos como tal fue creada por el matemático húngaro John Von Neumann (1903-1957) y por Oskar Morgenstern (1902-1976) en 1944 gracias a la publicación de su libro “The Theory of Games Behavior”. Anteriormente los economistas Cournot y Edgeworth habían anticipado ya ciertas ideas, a las que se sumaron otras posteriores de los matemáticos Borel y Zermelo que en uno de sus trabajos (1913) muestra que juegos como el ajedrez son resolubles. Sin embargo, no fue hasta la aparición del libro de Von Neumann y Morgenstern cuando se comprendió la importancia de la teoría de juegos para estudiar las relaciones humanas.
Von Neumann y Morgenstern investigaron dos planteamientos distintos de la Teoría de Juegos. El primero de ellos el planteamiento estratégico o no cooperativo. Este planteamiento requiere especificar detalladamente lo que los jugadores pueden y no pueden hacer durante el juego, y después buscar cada jugador una estrategia óptima.
En la segunda parte de su libro, Von Neumann y Morgenstern desarrollaron el planteamiento coalicional o cooperativo, en el que buscaron describir la conducta óptima en juegos con muchos jugadores. Puesto que éste es un problema mucho más difícil, sus resultados fueran mucho menos precisos que los alcanzados para el caso de suma cero y dos jugadores.
En los años 50 hubo un desarrollo importante de estas ideas en Princeton, con Luce and Raiffa (1957), difundiendo los resultados en su libro introductoria, Kuhn (1953) que permitió establecer una forma de atacar los juegos cooperativos, y por fin Nash (1950) quien definió el equilibrio que lleva su nombre, lo que permitió extender la teoría de juegos no-cooperativos más generales que los de suma cero. Durante esa época, el Departamento de Defensa de los EE.UU. fue el que financió las investigaciones en el tema, debido a que la mayor parte de las aplicaciones de los juegos de tipo suma-cero se concentraban en temas de estrategia militar.
John Forbes Nash (1928- ) es el nombre más destacado relacionado con la teoría de juegos. A los 21 años escribió una tesina de menos de treinta páginas en la que expuso por primera vez su solución para juegos estratégicos no cooperativos, lo que desde entonces se llamó "el equilibrio de Nash", que tuvo un inmediato reconocimiento entre todos los especialistas.
El punto de equilibrio de Nash es una situación en la que ninguno de los jugadores siente la tentación de cambiar de estrategia ya que cualquier cambio implicaría una disminución en sus pagos. Von Neumann y Oskar Morgenstern habían ya ofrecido una solución similar pero sólo para los juegos de suma cero. Para la solución formal del problema, Nash utilizó funciones de mejor respuesta y el teorema del punto fijo de los matemáticos Brouwer y Kakutani.
En los años siguientes publicó nuevos escritos con originales soluciones para algunos problemas matemáticos y de la teoría de juegos, destacando la "solución de regateo de Nash" para juegos bipersonales cooperativos. Propuso también lo que se ha dado en llamar "el programa de Nash" para la reducción de todos los juegos cooperativos a un marco no cooperativo. A los veintinueve años se le diagnosticó una esquizofrenia paranoica que lo dejó prácticamente marginado de la sociedad e inútil para el trabajo científico durante dos décadas. Pasado ese lapsus, en los años setenta, recuperó su salud mental y pudo volver a la docencia y la investigación con nuevas geniales aportaciones, consiguiendo en 1994 el Premio Nóbel de Economía compartido con John C. Harsanyi y Reinhart Selten por sus pioneros análisis del equilibrio en la teoría de los juegos no cooperativos.
En los 60 y 70 Harsany (1967) extendió la teoría de juegos de información incompleta, es decir, aquellos en que los jugadores no conocen todas las características del juego: por ejemplo, no saben lo que obtienen los otros jugadores como recompensa. Ante la multiplicidad de equilibrios de Nash, muchos de los cuales no eran soluciones razonables a juegos, Selten (1975) definió el concepto de equilibrio perfecto en el subjuego para juegos de información completa y una generalización para el caso de juegos de información imperfecta.
La última aportación importante a la teoría de juegos es de Robert J. Aumann y Thomas C. Schelling, por la que han obtenido el premio Nóbel de economía en el año 2005.
En The Strategy of Conflict , Schelling, aplica la teoría del juego a las ciencias sociales. Sus estudios explican de qué forma un partido puede sacar provecho del empeoramiento de sus propias opciones de decisión y cómo la capacidad de represalia puede ser más útil que la habilidad para resistir un ataque
Aumann fue pionero en realizar un amplio análisis formal de los juegos con sucesos repetidos. La teoría de los juegos repetidos es útil para entender los requisitos para una cooperación eficiente y explica por qué es más difícil la cooperación cuando hay muchos participantes y cuándo hay más probabilidad de que se rompa la interacción. La profundización en estos asuntos ayuda a explicar algunos conflictos, como la guerra de precios y las guerras comerciales.
APLICACIONES DE LA TEORIA DE JUEGOS
MERCADEO
Usted tiene un nuevo producto muy promisorio. ¿Debe usted lanzarse de primero al mercado? ¿Cosechará ganancias siendo pionero o le estará abriendo el camino a competidores cautos que se beneficiarán de sus errores?
Todos estas situaciones son opciones de juegos donde sus resultados dependerán no solamente de lo que usted haga sino también de lo que hagan sus competidores.
 Su empresa está en un mercado que cada día se estrecha más debido a la recesión de la economía y por la entrada de nuevos competidores. A medida que las ventas declinan, su principal competidor reduce precios y aumenta su producción. ¿Cuál debe ser su respuesta? ¿Lanzarse a una guerra de precios o mantenerse firme y perder ventas y participación de mercado? A situaciones como ésta se han enfrentado las aerolíneas, las revistas y los computadores personales entre otros.
Su empresa está en un mercado que cada día se estrecha más debido a la recesión de la economía y por la entrada de nuevos competidores. A medida que las ventas declinan, su principal competidor reduce precios y aumenta su producción. ¿Cuál debe ser su respuesta? ¿Lanzarse a una guerra de precios o mantenerse firme y perder ventas y participación de mercado? A situaciones como ésta se han enfrentado las aerolíneas, las revistas y los computadores personales entre otros. Producir una nueva generación de sus productos le representará inversiones cuantiosas en investigación y desarrollo. ¿Debe usted embarcarse en esto? Sus competidores se enfrentan a la misma situación. Si todos se lanzaran al mercado, ¿valdrá la pena participar en esta competencia donde si usted sale de primero el mercado podrá estar en corto tiempo tan saturado que su producto pionero le dará pérdidas? ¿O será mejor esperar por oportunidades de mercadeo en mercados más rentables?
ECONOMÍA

No debería sorprender que la Teoría de Juegos haya encontrado aplicaciones directas en economía. Esta triste ciencia se supone que se ocupa de la distribución de recursos escasos. Si los recursos son escasos es porque hay más gente que los quiere de la que puede llegar a tenerlos. Este panorama proporciona todos los ingredientes necesarios para un juego. Además, los economistas neoclásicos adoptaron el supuesto de que la gente actuará racionalmente en este juego. En un sentido, por tanto, la economía neoclásica no es sino una rama de la Teoría de Juegos.
RELACIONES INTERNACIONALES
RELACIONES INTERNACIONALES
También ha tenido una muy nutrida aplicación a raíz de que inicia precisamente como un instrumento de apoyo militar. Se han modelado casos de control o limitación de armamentos, ejercicios con pruebas nucleares, y amenazas o represalias ante determinadas acciones de países enemigos entre sí.
POLÍTICA

La Teoría de Juegos no ha tenido el mismo impacto en la ciencia política que en economía. Tal vez esto se deba a que la gente se conduce menos racionalmente cuando lo que está en juego son ideas que cuando lo que está en juego es su dinero. Sin embargo, se ha convertido en un instrumento importante para clarificar la lógica subyacente de un cierto número de problemas más paradigmáticos.
En la política ha enfatizado en los problemas de acción colectiva, de bienes públicos y de votaciones; y particularmente como insumo a la teoría de las decisiones interdependientes, es una herramienta poderosa para modelar el comportamiento político.
BIOLOGÍA
En Biología se ha utilizado ampliamente la teoría de juegos para comprender y predecir ciertos resultados de la evolución, como lo es el concepto de estrategia evolutiva estable introducido por John Maynard Smith en su ensayo "Teoría de Juegos y la Evolución de la Lucha", así como en su libro "Evolución y Teoría de Juegos".
FILOSOFÍA
Los especialistas en Teoría de Juegos creen que pueden demostrar formalmente por qué incluso el individuo más egoísta puede descubrir que con frecuencia, cooperar con sus vecinos en una relación a largo plazo redundará en su propio interés ilustrado.
Con este fin estudian los equilibrios de juegos con repetición (juegos que los mismos jugadores juegan una y otra vez). Pocas cosas han descubierto en esta área hasta el presente que hubieran sorprendido a David Hume, quien hace ya unos doscientos años articuló los mecanismos esenciales. Estas ideas, sin embargo, están ahora firmemente basadas en modelos formales. Para avanzar más, habrá que esperar progresos en el problema de la selección de equilibrios en juegos con múltiples equilibrios. Cuando estos progresos se den, sospecho que la filosofía social sin Teoría de Juegos será algo inconcebible – y que David Hume será universalmente considerado como su verdadero fundador.
Algunas otras aplicaciones de la Teoría de Juegos a la vida real son las siguientes:
-Contratos
-Guerras militares
-Guerras comerciales
-Marketing para la competencia en los mercados
-Negociaciones domésticas
-Negociaciones comerciales
-Negociaciones colectivas
-Alianzas
BIENES PUBLICOS
Ha sido común en Latinoamérica encontrar peticiones incesantes de los entes públicos –nacionales, federales o locales- que administran el procesamiento y distribución del agua, para restringir el desperdicio en aras de eventuales déficit en el preciado líquido. La construcción de incentivos –positivos y negativos- para evitar el desperdicio transcurre precisamente por el estudio estratégico y la debida modelización del porqué la
población no protege bienes públicos y de cómo fomentar el control social sobre el posible agotamiento de tales bienes.
FUNDAMENTOS
Teoría de juegos
En esencia es una técnica para tomar decisiones en situaciones de conflicto sobre la base de la construcción de una matriz formal que permite comprender el conflicto y sus posibles soluciones. Su aplicación es apropiada para problemas donde quienes toman las decisiones no poseen un control completo de los factores que influyen en el resultado, pero dónde se presentan influencias y determinaciones mutuas en las actuaciones reciprocas de los individuos u organizaciones sociales involucrados. La teoría de juegos tiene una relación muy lejana con la estadística. Su objetivo no es el análisis del azar o de los elementos aleatorios sino de los comportamientos estratégicos de los jugadores.Un ejemplo es la figura que se muestra acontinuacion juego de la ruleta.
Tomado Pagina hospedada en el servicio personales.com de servitec
Valor del juego
Se llama al valor del juego al pago que un jugador tiene garantizado que puede recibir de un juego si toma una decisión racional, independientemente de las decisiones de los demás jugadores. Ningún jugador aceptará formar parte de una coalición si no recibe como pago al menos el valor del juego.
Paraboloide hiperbólico
Al paraboloide hiperbólico también se lo denomina silla de montar por su gráfica. Tiene la peculiaridad de contener rectas en su superficie.Estos criterios sirven para obtener la solución de un juego y determinar la estrategia óptima de un jugador:
Criterio Maximín: Identifica los mínimos por renglón y selecciona el mayor.
Criterio Mínimax: Identifica los máximos por columna y selecciona el menor.
Si el valor maximín del primer jugador es igual al mínimax del segundo jugador, entonces el juego es de estrategia pura (existe un punto de silla de montar). El valor del juego para el primer jugador es su valor maximín.
Por ejemplo: Dos gasolineras se encuentran una frente a la otra.
Los consumidores están pendientes del precio y cada gasolinera debe decidir si cobra un precio alto o uno bajo. La matriz de recompensas es la siguiente:
Resolviendo y aplicando los criterios maximín y minimax:
Dado que el valor maximín del primer jugador es igual al mínimax del segundo jugador, entonces el juego es de estrategia pura (existe un punto de silla de montar). Ambos jugadores escogen bajar sus precios. El valor del juego para el primer jugador es 0 y para el segundo jugador también.
Tomado Pagina hospedada en el servicio personales.com de servitec
Matriz de pago
Es una matriz que resume la información dada por las funciones de pago en un juego rectangular o en un juego extensivo en su forma normal.
Ejemplo.
Consideremos el juego piedra, papel o tijera, donde el perdedor debe pagar una unidad monetaria al ganador y en caso de empate no hay pago para ninguno. La siguiente tabla puede considerarse una matriz de pagos para el juego:
Si numeramos las estrategias piedra, papel y tijera como 1, 2 y 3 respectivamente, la matriz de pagos será por definición:
Tomado Pagina hospedada en el servicio personales.com de servitec
Estrategia
Una estrategia es la descripción completa de una forma determinada de jugar, dependiente de lo que hacen los demás jugadores y de la duración del juego. Para cualquier juego entre dos personas, se puede representar cada secuencia posible del juego como una casilla en una tabla. La tabla deberá poseer tantas filas como estrategias tenga un jugador, y una columna por cada estrategia del otro jugador. Si se estructura un juego de esta manera, se dice que está en forma normal.
JUGADOR UNO | |||
ESTRATEGIA 1 | ESTRATEGIA 2 | ||
JUGADOR DOS | ESTRATEGIA 1 | XXXXXX | XXXXXX |
ESTRATEGIA 2 | XXXXXX | XXXXXX | |
Tomado Pagina hospedada en el servicio personales.com de servitec
Estrategia Aleatorizado
Es una combinación de dos estrategias escogidas a azar, una cada vez, según determinadas probabilidades, en contraste con una estrategia pura que no contiene tales elementos de azar.
Ejemplo: Suponga el siguiente juego:
Resolviendo y aplicando los criterios maximín y minimax:
Se observa que el valor minimax de un jugador 2 no es igual al maximín del jugador 1. El jugador 2 selecciona la estrategia A y el jugador 1 la estrategia X.
Estrategia dominante
Se dice que un jugador posee una estrategia dominante si una estrategia particular es preferida a cualquier otra estrategia a disposición de él. Es posible que cada uno de los dos jugadores tenga estrategia dominante.
Ejemplo: Observe la siguiente matriz de resultados:
Independientemente de lo que haga el Jugador 1, para el jugador 2 siempre será preferible la estrategia X. Se dice que la estrategia X domina a la estrategia Y. el jugador 2 nunca escogerá la estrategia Y.
Tomado Pagina hospedada en el servicio personales.com de servitec
Juego de suma cero
Son los juegos dónde un jugador gana sólo si el otro pierde y no es posible cooperación alguna (y dónde de alguna manera se genera una «guerra abierta»). El mejor ejemplo de esto es el póquer, donde los jugadores ponen el dinero en el centro, y alguien se lo lleva todo cuando gana. Nadie gana un solo peso que otro no haya perdido. La mayoría de los juegos de ocio son de tipo suma cero. Es válido incluso para aquellos en los que no interviene el dinero.
JUGADORES | JUGADOR B | ||
JUGADOR A | Estrategias | B1 | B2 |
A1 | -X | X | |
A2 | Y | Y | |
Tomado Pagina hospedada en el servicio personales.com de servitec
Tomado Pagina hospedada en el servicio personales.com de servitec
Punto de silla
Un punto de silla es un pago que es simultáneamente un mínimo de su renglón y un máximo de su columna. Para encontrar puntos de silla, Encierre en círculo los mínimos de todos los renglones y meta en caja las máximas de todas las columnas. Los puntos de silla son aquellas entradas que son simultáneamente en círculo y en caja.
Un juego es estrictamente determinado si tiene por lo menos un punto de silla. Las siguientes declaraciones se aplican a los juegos estrictamente determinados:
Todos los puntos de silla en un juego tienen los mismos valores de pago.
Elegir el renglón y la columna que pasan por cualquier punto de silla de estrategias minimax para ambos jugadores. Es decir, el juego es solucionado por el uso de estas estrategias puras.
El valor de un juego estrictamente determinado es el valor del punto de silla. Un juego justo tiene un valor igual a cero, si no, es injusto o parcial.
Ejemplo
En el juego más arriba, hay dos puntos de silla, mostrados en color.
Pues son cero los puntos de silla, es un juego justo.
Tomado Última actualización: septiembre 2007
Derechos de autor © Stefan Waner
Derechos de autor © Stefan Waner
DESARROLLO CONCEPTUAL
El juego de los dos dedos cuando esta estrictamente determinado
Formulación de juegos de dos personas con suma cero
Para ilustrar las características básicas de un modelo de teoría de juegos, considérese los juegos llamados pares e impares. Éste consiste nada más en que los dos jugadores muestran al mismo tiempo uno o dos dedos. Si el número de dedos coincide, el jugador que apuesta a pares (por ejemplo, el jugador 1) gana la apuesta al jugador que va por impares (jugador II). Si el número no coincide, el jugador 1 pierde y le paga al jugador II. Entonces, cada jugador tiene dos estrategias: mostrar uno o dos dedos.
JUGADOR 1 | JUGADOR 2 | |||
Ec1 | Ec2 | Mínimo | ||
Er1 | 6 | -11 | -11 | |
Er2 | 3 | 2 | 2 | |
Máximo | 6 | 2 | ||
Este juego se encuentra estrictamente determinado por que tiene punto de silla, donde este es el valor esperado del juego es decir en la intersección de en la intersección de la mí Er2;Ec2 se encuentra:
El punto de silla = valor del juego = 2
En general, el juego de dos personas se caracteriza por
1. Las estrategias del jugador I.
2. Las estrategias del jugador II.
3. La matriz de pagos.
Características
· Antes de iniciar el juego, cada jugador conoce las estrategias de que dispone, las que tiene su oponente y la matriz de pagos.
· Una jugada real en el juego consiste en que los dos jugadores elijan al mismo tiempo una estrategia sin saber cuál es la elección de su oponente.
· Una estrategia puede constituir una acción sencilla, como mostrar un número par o impar en dedos en el juego de pares e impares.
· Por otro lado, en juegos más complicados que llevan en sí una serie de movimientos, una estrategia es una regla predeterminada que especifica por completo cómo se intenta responder a cada circunstancia posible en cada etapa del juego.
· Por lo general, la matriz de pagos muestra la ganancia (positiva o negativa) que resultaría con cada combinación de estrategias para el jugador 1. Se da de esta manera, ya que la matriz del jugador II es el negativo de ésta, debido a la naturaleza de la suma cero del juego.
· Los elementos de la matriz pueden tener cualquier tipo de unidades, como dólares, siempre que representen con exactitud la utilidad del jugador 1 en el resultado correspondiente.
· Por otro lado, el resultado que corresponde a un elemento 2 en una matriz de pagos debe "valer el doble" para el jugador 1 que el resultado correspondiente a un elemento 1. Así, dada la elección, debe serle indiferente un 50% de posibilidades de recibir el primer resultado (en lugar de nada) y recibir en definitiva el último resultado.
· Un objetivo primordial de la teoría de juegos es establecer criterios racionales para seleccionar una estrategia, los cuales implican dos suposiciones importantes:
o Ambos jugadores son racionales.
o Ambos jugadores eligen sus estrategias sólo para promover su propio bienestar (sin compasión para el oponente).
El juego de los dos dedos cuando no esta estrictamente determinado
I | II | Mínimo | |
I | -2 | 3 | -2 |
II | 3 | -4 | -4 |
Máximo | 3 | 3 |
P1, (1-P1)
Como se puede notar no hay ninguna coincidencia en los números es decir no hay punto de silla entonces procedemos ha hallar las probabilidades con el que jugadores debe jugar.
Estrategias del jugador renglón
Multiplicación de matrices
P1, (1-P1) = -2P1+3(1-P1); 3P1-4(1-P1)
VEJ= (-2P1+3-3P1); (3P1-4+4P1)
VEJ= -5P1+3; 7P1-4
Ecuación 1 = -5P1+3
Ecuación 2 = 7P1-4
· Se le da valores arbitrariamente a P1 en la ecuación 1
Si P1=0 entonces; -5(0)+3=3
Si P1=1 entonces; -5(1)+3=-2
· Se le da valores arbitrariamente a P1 en la ecuación 2
Si P1=0 entonces; 7(0) -4 = -4
Si P1=1 entonces; 7(1) -4 = 3
Es decir;
-5P1+3 = 7P1-4
-5P1-7P1=-4-3
-12P1=-7
P1=-7/-12
P1= 0.5833
P2=1-P1
P2=1-0.58
P2=0.42
Las probabilidades con la que debe jugar el jugador renglón, es del 58% con la estrategia I y del 42% con la estrategia II.
Estrategias del jugador columna
P1, (1-P1) = -2P1+3(1-P1); 3P1-4(1-P1)
VEJ= (-2P1+3-3P1); (3P1-4+4P1)
VEJ= -5P1+3; 7P1-4
Ecuación 1 = -5P1+3
Ecuación 2 = 7P1-4
· Se le da valores arbitrariamente a P1 en la ecuación 1
Si P1=0 entonces; -5(0)+3=3
Si P1=1 entonces; -5(1)+3=-2
· Se le da valores arbitrariamente a P1 en la ecuación 2
Si P1=0 entonces; 7(0) -4 = -4
Si P1=1 entonces; 7(1) -4 = 3
Es decir;
-5P1+3 = 7P1-4
-5P1-7P1=-4-3
-12P1=-7
P1=-7/-12
P1= 0.5833
P2=1-P1
P2=1-0.58
P2=0.42
Las probabilidades con la que debe jugar el jugador columna son las misma que de jugador renglón en la utilización de estrategias, es decir del 58% con la estrategia I y del 42% con la estrategia II.
FUENTE: adaptado por los estudiantes de octavo semestre de ingeniería industrial universidad libre seccional Barranquilla; de la Última actualización: septiembre 2007 Derechos de autor de la pagina de © Stefan Waner
Dinámica para encontrar el valor del juego cuando no está estrictamente determinado
Cuando un juego no tiene punto de silla, la teoría de juegos aconseja a cada jugador asignar una distribución de probabilidad sobre su conjunto de estrategias. Vamos a expresar esto de la siguiente forma:
Xi = probabilidad de que el jugador A use la estrategia i ( i = 1,2,…,m)
yi = probabilidad de que el jugador B use la estrategia j ( j = 1,2,…,n) donde n y m son los números de estrategias disponibles.
Vamos a empezar con el juego (2 x n) en el que el jugador A tiene dos estrategias, siendo la recompensa para este mismo jugador.
Suponemos que el jugador A mezcla las estrategias A1 y A2 con sus probabilidades respectivas x1 y 1 – x1, siendo 0 ≤ x1 ≤ 1. A su vez el jugador B mezcla sus estrategias con sus respectivas probabilidades.
En este caso, la recompensa esperada por A correspondiente a la j-ésima estrategia pura de B se calcula de la siguiente manera:
(a1j – a2j) x1 – a2j, j = 1,2,…,n
El jugador A trata así de determinar el valor de x1 que maximice las recompensas mínimas esperadas:
Max min {(a1j – a2j)x1 – a2j}
Tenemos un juego de 2 x 4 en el que la recompensa es para el jugador A.
B1 | B2 | B3 | B4 | Mínimo | |
A1 | -1 | 2 | 2 | 3 | -1 |
A2 | 6 | 4 | 3 | 2 | 2 |
Máximo | 6 | 4 | 3 | 3 |
No hay punto de silla es decir el juego no está estrictamente determinado, no hay solución de estrategia pura, por lo que debemos mezclar estrategias. Las recompensas esperadas por A correspondientes a las estrategias puras de B, son:
RELACION DE ECUACIONES |
|Estrategia pura de B |Recompensa esperada por A | |
|1 |-2x1 + 4 | |
|2 |-x1 + 3 | |
|3 |-x1 + 2 | |
|4 |-7x1 + 6 | |
Se iguala las ecuaciones número 2 y 4 y nos resulta lo siguiente
-x1+3=-7x1+6
-x1+7x1=6-3
6x1=3
X1=3/6
X1=0.5
La solución óptima del jugador A mezcla A1 y A2 con las probabilidades 0.5 y 0.5, respectivamente. El valor V correspondiente del juego se determina sustituyendo x1 = 0.5 en cualquiera de las funciones de las líneas B3 y B4, con lo que se obtiene:
V = 0.5 + 2 = 2.5
V = -7(0.5) + 6= 2.5
Fuente: Tomado Última actualización: septiembre 2007
Derechos de autor © Stefan Waner
Dinámica para el encontrar el valor del juego cuando esta estrictamente determinado
Para determinar si un juego está estrictamente determinado debemos saber si tiene punto de silla y esto se sabe Cuando hayamos los mínimos en los reglones y los máximos en la columna loa cuales arrojara unos valores que al ser comparados mostrara una igualdad de unos de esos valores tanto en columna como en renglón donde estos se intercepta será nuestro punto de silla y demostrara que el juego está estrictamente determinado siendo este el valor del juego.
Un punto de silla es un pago que es simultáneamente un mínimo de su renglón y un máximo de su columna. Para encontrar puntos de silla, Encierre en círculo los mínimos de todos los renglones y meta en caja las máximas de todas las columnas. Los puntos de silla son aquellas entradas que son simultáneamente en círculo y en caja.
Un juego es estrictamente determinado si tiene por lo menos uno punto de silla. Las siguientes declaraciones se aplican a los juegos estrictamente determinados:
- Todos los puntos de silla en un juego tienen los mismos valores de pago.
- Elegir el renglón y la columna que pasan por cualquier punto de silla de estrategias minimax para ambos jugadores. Es decir, el juego es solucionado por el uso de estas estrategias puras.
El valor de un juego estrictamente determinado es el valor del punto de silla. Un juego justo tiene un valor igual a cero, si no, es injusto o parcial.
Ejemplo dilema del prisionero
Se arresta a dos sospechosos por robo, y si se les condena, cada uno recibiría una sentencia de 10 años. Sin embargo, si ninguno confiesa, la evidencia bastaría para una sentencia de 1 año por posesión de bienes robados. Se interroga a cada sospechoso por separado y no se permite comunicación entre ellos. El fiscal promete impunidad al que confiese, pero la totalidad de la sentencia de 10 años al que no confiese. Si confiesan ambos, cada uno obtiene una sentencia reducida de 5 años. La matriz de rendimiento para este caso sería:
La mejor estrategia para cada sospechoso es confesar, sin importar lo que haga el otro.
FUENTE: Tomado Última actualización: septiembre 2007 Derechos de autor © Stefan Waner
Reducción de una matriz
Una acción domina a otra si todos sus pagos son por lo menos tan provechosos al jugador que los pagos correspondientes de la otra. En términos de la matriz de pagos, podemos decirlo como sigue:
- Renglón r en la matriz de pagos domina a renglón s si cada pago en renglón r ≥ el pago correspondiente en renglón s.
- Columna r en la matriz de pagos domina a columna s si cada pago en columna r ≤ el pago correspondiente en columna s.
Observe que si dos renglones o columnas son iguales, cada uno domina al otro. Un renglón o columna domina estrictamente a un otro si el uno domina al otro y son desiguales.
Siguiendo el primero principios de la teoría de juegos, la acción que corresponde a un renglón o columna estrictamente dominado nunca será jugado, y ambos jugadores son conscientes de esto por el segundo principio. Entonces cada jugador quien sigue los principios de la teoría de juegos eliminará repetidamente renglones y columnas dominadas como podría ser el caso. (En el caso que son iguales dos renglones o columnas, no hay razón para elegir uno sobre el otro, entonces cualquiera de los dos puede ser eliminado.) Este proceso se llama reducción por predominio.
Ejemplo
Considere otra vez el siguiente juego.
Acción Columna | ||||||
A | B | C | ||||
Acción Renglón | 1 | 0 | -1 | 1 | ||
2 | 0 | 0 | 2 | |||
3 | -1 | -2 | 3 | |||
Pues las entradas de Renglón 2 son ≥ las entradas correspondientes en Renglón 1, entonces Renglón 2 domina a Renglón 1.
Pues las entradas de Columna B son ≤ las entradas correspondientes en Columna A, Columna B domina a Columna A.
Reducir el juego más arriba por predominio
Pues Renglón 2 domina a Renglón 1, eliminamos Renglón 1 para obtener
A | B | C | |||
2 | 0 | 0 | 2 | ||
3 | -1 | -2 | 3 |
Pues Columna B ahora domina a ambas Columnas A y C, eliminamos las dos Columnas A y C para obtener
B | |||
2 | 0 | ||
3 | -2 |
Pues el primero renglón domina ahora al último renglón, eliminamos el último renglón, y estamos reducidos a la siguiente matriz 1×1
B | |||
2 | ( | 0 | ) |
En este caso, hemos solucionado el juego por reducción por predominio: El jugador renglón debe siempre jugar 2 y el jugador de columna debe siempre jugar B. Pues el pago correspondiente es 0, decimos que el juego es justo (ninguno jugador tiene ventaja sobre el otro).
Observe que tuvimos suerte aquí: No todos los juegos pueden ser reducido a un juego 1×1 por predominio.
FUENTE: Tomado Última actualización: septiembre 2007 Derechos de autor © Stefan Waner
Solución por Programación lineal
Pasos del método de la programación lineal para determinar la estrategia aleatorizada Óptima.
1. Determine la matriz de recompensa R.
2. Si R tiene elementos no positivos, forme Rʼ sumando una constante a cada elemento de R. Si E y Eʼ constituyen los valores esperados del juego asociados con las matrices de recompensa R y Rʼ, respectivamente, entonces Eʼ = E + (La Constante añadida).
3. Si el jugador renglón adopta una estrategia aleatorizada, donde las probabilidades de selecciones de los renglones 1 a n son P1 a Pnʼ respectivamente, entonces:
Pr = [ P1 P2 …. Pn ] donde P1 + P2 +…. + Pn = 1
Si el jugador columna adopta una estrategia pura, los valores esperados de dichas estrategias puras se incluyen en la matriz.
E (Pura)= Pr * Rʼ
Calcule E (Pura)
4. Resuelva P1 + P2 +…. + Pn = 1 para Pn = 1 y sustituya el resultado en E (Pura).
5. El valor esperado Eʼ del juego es menor o igual que cada uno de los elementos de la matriz del paso 4. Cada una de esas desigualdades resultantes constituye una restricción en el problema de programación lineal. Liste estas restricciones.
6. Cada una de las probabilidades P1, P2, P3 , … debe ser menor o igual que 1. Liste estas restricciones.
7. Establezca el objetivo, que consiste en obtener el valor máximo de Z= Eʼ.
8. Resuelva el problema de programación lineal y determine los valores de P1 P2 …. Pn, y Eʼ.
9. Describa la estrategia aleatorizada óptima del jugador renglón proporcionando la probabilidad con la que el jugador debería elegir cada renglón.
10. Reste la constante del paso 2 de Eʼ para obtener E, el valor esperado del juego.
EJEMPLO: JUEGO DE DOS JUGADORES DE SUMA NULA
FUENTE: tomado del libro de winston en su pagina 545
Solución por Solver
Lo ejercicios de teoría de juego que no están estrictamente determinada se le puede dar solución por medio de la herramienta informática solver que es uno de los complementos de la hoja de cálculo Excel.
Pasos para la resolución de problemas en solver:
1. se plantea la matriz de juego en la hoja de cálculo de Excel
2. Se halla los mínimos de los renglones y los máximos en las columna a través de las formulas de Excel MIN y MAX llevando el cursor al reglón de debajo del reglón mínimo colocando el signo igual del teclado seguramente escribiendo la función o formula MIN y seleccionando las celadas de la Er1 y terminando con un enter y luego desplazando la copia de esta función hasta donde sea necesario. Igualmente para hallar los máximos de la columna se llevara el cursor al lado de la columna que dice máximo e insertamos la función MAX MIN y seleccionando las celadas de la Ec1 y terminando con un enter y luego desplazando la copia de esta función hasta donde sea necesario.
3. Tomamos dos columnas hacia la izquierda donde una de ellas va ser nombradas con el número de probabilidades iguales a las de las estrategias y la siguiente a ella rellenada con ceros, al llegar al rellenar todas las columna de ceros correspondiente al número de probabilidades en la casilla siguiente de la columna se establece la sumatoria de todas estas probabilidades a través de la función autosuma ubicada en la ventana de inicio del lado derecho.
4. luego establecemos debajo de la matriz de pago un pequeña matriz renglón donde ubicaremos las suma y producto de la matriz de pago con las probabilidades atravez de la función de Excel SUMAPRODUCTO llevamos el cursor se lleva al renglón de abajo se digita el símbolo igual y digitamos la función segundo de la selección de la matriz de probabilidades se fijan con la tecla F4 separados por un punto y coma y se selecciona la matriz de pago y se da enter, y luego desplazamos esta casilla seleccionada para que me arroje la suma produce de las demás estrategias. Luego tomamos una casilla cualquiera llamadas valor esperado del juego.
5. ya planteada la estructura del ejercicio se procede a la utilización del solver donde se procederá al llenado de los siguientes comandos en el valor esperado del juego en la casilla inmediata seguida va ser nuestra celda objetivo, luego como vamos a hallar las probabilidades de mi jugador renglón se selecciona el máximo, después la celdas a cambiar será las de las probabilidades y la celda objetivo, además este ejercicio va estar sujeto a las siguientes restricciones: a) la sumatoria de mis probabilidades va ser igual a uno (1). b) las probabilidades deben ser mayores o iguales a ceros. c) la suma producto de mis estrategias con las probabilidades deben ser mayores a la de mi celda objetivo.
Luego de haber gestionado todos estos comandos nos vamos al botón opciones y se adopta no negativos, se le da cerrar, luego resolver y por ultimo seleccionamos utilizar solución de solver y aceptar. Y todo esto nos arroja los resultados de las probabilidades con las que debe jugar mi jugador renglón.
6. para encontrar las probabilidades con la que debe jugar mi jugador renglón procedemos a cambiar en solver lo siguiente en el valor de función objetivo seleccionamos mínimo y en las restricciones se cambia que los sumaproductos serán menores que la celda objetivo o valor esperado en el juego.
Para realizar los ejercicios debe seguir los siguientes pasos:
-Activar Solver
Si no esta activado haga clic en el Botón de Office
Opciones de Excel-Después de haber activado Solver y tener las plantillas de los ejercicios sea para el jugador columna o para el jugador fila.
Complementos
Elegir opción Administrar: Complementos de Excel y pulsar Ir
Activar Solver
Plantilla jugador Renglón
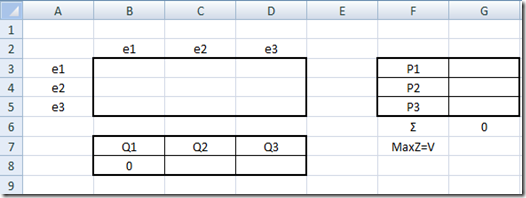
Plantilla jugador Columna

-Después de tener la plantilla, en la celda de los valores esperados Q debemos colocar la función =SUMAPRODUCTO(de las proporciones;Columnas) en cada uno de los valores esperados.
Plantilla jugador renglón

Plantilla jugador Columna
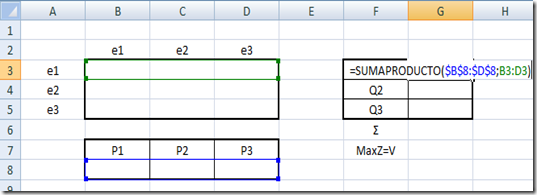
-La Sumatoria Ʃ es =SUMA(proporciones)
Plantilla jugador Renglón
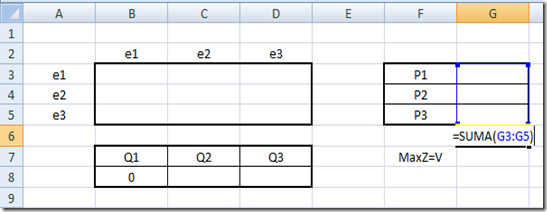
Plantilla jugador Columna

-Seguidamente nos vamos a la función Solver Elegimos La función Objetivo que es:
MaxZ=V Si queremos maximizar-Las Celdas que van a buscarle los valores son: Las Proporciones y La Celda Objetivo
MinZ=V Si queremos minimizar

-Restricciones Son las Siguientes
MAXIMIZAR
* Ʃ=1
* (Q1,Q2,Q3) >= MaxZ=V
* (P1,P2,P3) >= 0
MINIMIZAR
* Ʃ=1
* (Q1,Q2,Q3) <= MaxZ=V
* (P1,P2,P3) >= 0
-Opciones:
Adoptar modelo lineal-Resolver
Adoptar no negativo
Aceptar

Ejercicios Propuestos
Ejercicios Propuestos
Ejercicios Resueltos de los propuestos

















